
Research
After Goldman – Trouble Getting to Class
Key Points Fideres has analyzed a sample of 10b-5 filings to determine the impact of the Supreme Court’s 2021 Goldman ruling. We find that, sinc...

Historically, courts have hesitated to award damages to plaintiffs in data breach and data misuse cases because of a lack of a clear theory of harm. Plaintiffs who have not been directly and provably affected by credit card fraud have generally not suffered a direct monetary loss.
The premise of the recent Lloyd v. Google decision in the UK is that data subjects possess their personal data in the manner of an economic asset. Anyone using this data without the subject’s permission has deprived them of control over this asset. This “loss of control” suggests that data breach victims are entitled to a form of damages known as “user” or “negotiating” damages. Harm in such a case stems from the idea that the owner of an asset ought to be able to decide the terms on which he or she is willing to lend it out for others’ use.
Crucially, for the question of data valuation, this right exists even if the proposed use of the asset does not damage or use it up. Under user damages, there is no need for the owner to demonstrate that they have been directly harmed, merely that they have been deprived of control of their property. In principle, the harmed party was unlawfully denied the opportunity to bargain with the “user” of his or her property.
The “user damages” framework, as a legal precept, establishes that personal data valuation can be framed as the outcome of a negotiation between the owner of the personal data, i.e. the data subject herself, and the infringer who used this information without consent, i.e., a first or third-party data collector such as Google.
As it turns out, the problem of modeling a hypothetical negotiation between two parties has been articulated at length in game theory and microeconomics. The classic approach is to estimate a result known as the Nash bargaining solution (“NBS”), which resolves the negotiation by choosing the only outcome that satisfies a series of mathematical assumptions about the options and preferences of each party.
The key insight of the NBS framework lies in posing all negotiations as a discussion over how to split up the rewards of a collective venture. Suppose that two parties can either
Under these conditions, neither party will accept any division of the pot that results in a worse outcome than their status quo option, because if either party tried to force such an outcome, the other party would simply walk away from the negotiation.
An important implication is that the range of possible negotiating outcomes is not determined by any questions of how much “value” each party adds. Instead, NBS is only interested in three things: the collective total value of the agreement, and the value that each party would realize in the absence of an agreement.
Even without further elaboration, this relatively simple and intuitive framework clarifies a few crucial points about the nature of the hypothetical negotiation. It defines the stakes of the bargaining and puts firm upper and lower boundaries on the outcome of the hypothetical negotiation.
As discussed above, the NBS requires only three pieces of information to put upper and lower boundaries on how much the data collector might have paid: the value of the status quo outcome for the individual, the value of the status quo outcome for the data collector, and the total value that can be realized if the individual allows her data to be used.
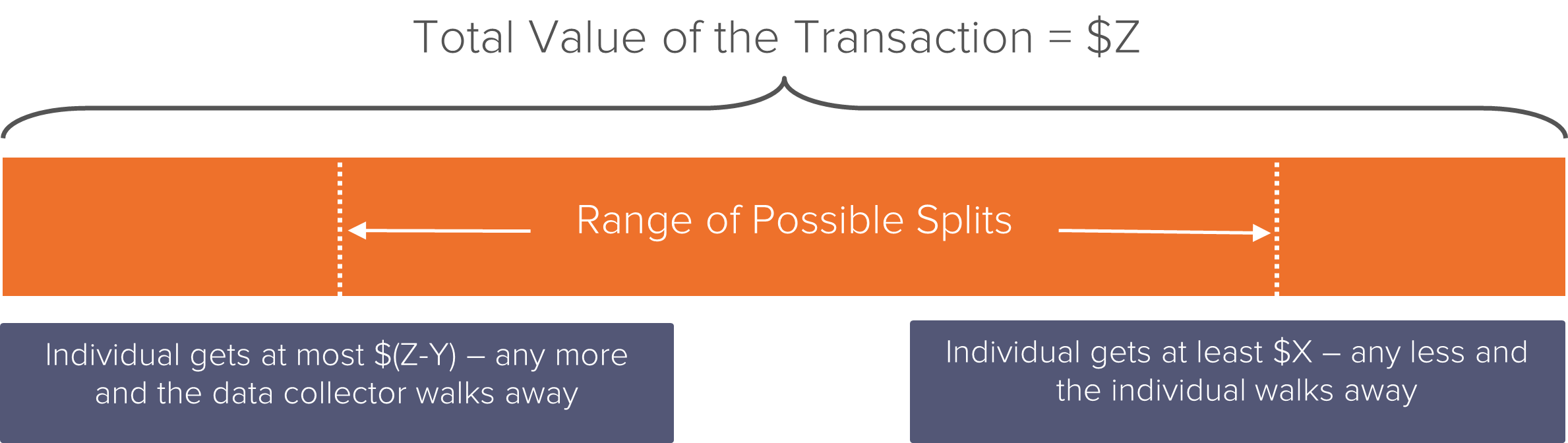
From these parameters, we estimate that the amount that the data collector might have paid the individual for her data, had she been afforded the opportunity to bargain for it, falls somewhere between $X and $(Z-Y).
These bounds hold regardless of the external conditions of the bargaining, such as the impatience or beliefs of the two parties. In the original framework proposed by Nash, the assumption of symmetric time-preferences and information leads to a unique point within this range that “solves” the bargaining model. This is the point which maximizes the “Nash Product,” which is given by the formula
(S1 – Q1)(S2 – Q2)
where S1 and S2 represents the utility value of the share received by each of the parties, while Q1 and Q2 represent the utility value of each party’s status quo options. Solving for this maximum in the example given above, for instance, results in an NBS of (X + (Z-Y))/2.
The basic version of the bargaining model discussed above has seen several elaborations and extensions since the initial publication of Nash’s pathbreaking paper in 1950. A commonly used extension of the model, for instance, is to relax the assumption that both parties have the same degree of time-sensitivity and of information. This results in the more generalized “asymmetrical” Nash product given by the formula
(S1 – Q1)β (S2 – Q2)1 – β
where β is a number between 0 and 1 that represents the bargaining power of the first party in the negotiation. Where both parties have the same bargaining power, β = 50%, and the solution is identical to the standard “symmetrical” case. Where the first party has higher (or lower) bargaining power than the second party, β shifts up (or down) and the solution shifts away from (or toward) that party’s lower bound.
Further elaborations involve game-theoretic “sequential” bargaining models, known as Rubenstein models, in which parties make offers and counter-offers over a hypothetically infinite period of time. These models are popular in the academic literature because they quantify the advantages of time-sensitivity and because they have a game-theoretic “equilibrium” solution. Like the asymmetric Nash product models, they are based on the same fundamental underlying framework.
The bargaining model proposed here, in combination with the ‘user damages’ theory of harm, may represent a way forward in valuing personal data for litigation in the US and the UK. A hypothetical negotiation between plaintiffs or claimants and an infringer would not require individualized analysis of harm nor, indeed, individual proof of harm (though establishing a class wide figure for the valuation of privacy, for instance, might prove more difficult). The NBS, for its part, represents an intuitive and lightweight model with low data requirements that could help to balance the respective economic positions of the litigants in data breach cases and beyond.
Max joined Fideres in 2016. He has led the development and implementation of economic models for major collective actions in the US and the UK, contributing to litigation on a variety of topics. His reports and econometric work has been included in cases for conduct including, among others, the FX and LIBOR benchmark manipulation, digital market monopolisation by Apple and Amazon, and consumer claims against a cartel of US generic drug manufacturers, abuse of market power by large regional US hospital systems, restriction of the right to repair by John Deere, and the combined abuse of dominance by Visa and Mastercard in UK payment systems. Before joining Fideres, Max worked at the national laboratory in Los Alamos, New Mexico, as part of a team designing neural networks for applications in machine learning. Max holds an MSc in Economic History from the London School of Economics.

Key Points Fideres has analyzed a sample of 10b-5 filings to determine the impact of the Supreme Court’s 2021 Goldman ruling. We find that, sinc...


Fideres investigation sheds light on UK Energy Suppliers Discriminating Against the Most Vulnerable Households


Trends in US antitrust litigation.


London: +44 20 3397 5160
New York: +1 646 992 8510
Rome: +39 06 8587 0405
Frankfurt: +49 61 7491 63000
Johannesburg: +27 11 568 9611
Madrid: +34 919 494 330